Управление образования и науки Запорожской обладминистрации

Запорожский областной институт последипломного педагогического образования

ІІІ этап 53 Всеукраинской олимпиады по математике 2012-2013 г.

7 класс

 1. Два брата пошли в поход. Веня взял с собой три банки сгущёнки, а Сеня только две. Вечером они встретили грибника и вместе с ним съели всю сгущёнку. Всем досталось поровну. Грибник за это дал братьям пять грибов. Как нужно справедливо поделить грибы между братьями?

 

2. В алфавите языка племени АУ всего две буквы: А и У. В результате следующих замен сочетаний букв смысл любого слова не изменяется:

УАУ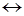АА, УАА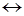АУ, ААУ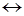УА, ААА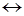УУ

(замену можно делать в любом месте слова). Одинаков ли смысл у слов УАА и АУУ?

 

3. На острове живут рыцари, которые всегда говорят правду, и лжецы, каждое утверждение которых ложно. Путник встретил троих островитян и спросил каждого из них: «Сколько рыцарей среди твоих спутников?» Первый ответил: «Ни одного». Второй сказал: «Один». Что сказал третий?

 

4. Играют двое. На столе лежат по одной монете достоинством 1, 2, 3, 5, 10, 20 и 50 копеек, а в кассе имеется неограниченный запас монет всех видов. За один ход разрешается взять любую монету со стола, разменять ее на более мелкие, и положить их на стол. Проигрывает тот, кто не сможет сделать ход. Кто выиграет при правильной игре?

 

5. Иванушка увидел двух двухголовых дракончиков, головы которых спутались. Драконы бывают либо правдивые, все головы которых говорят только правду, либо лживые, все головы которых всегда лгут. Головы сказали следующее:

Первая голова: «Я — правдивая голова».

Вторая голова: «Третья голова — моя родная голова».

Третья голова: «Вторая голова — не родная мне голова».

Четвёртая голова: «Третья голова — лживая».

Какая голова родная первой голове?

 

8 класс

 

1. Окружность разбита на 12 равных частей. В каждой из точек деления записано по числу. Известно, что сумма трёх чисел в вершинах любого равнобедренного треугольника - целое число. Верно ли, что сумма трёх чисел в вершинах любого треугольника - тоже целое число?

 

2. На гранях куба написаны натуральные числа, а в каждой вершине – произведения чисел на трех гранях с этой вершиной. Найдите сумму чисел на гранях, если сумма в вершинах равна 70.

 

3. Клетки квадратной таблицы 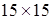 раскрашены в красный, синий и зеленый цвета. Докажите, что найдутся по крайней мере две строки, в которых клеток хотя бы одного цвета поровну.

 

4. Вовочка сдает компьютерный тест, состоящий из 6 вопросов, на каждый из которых нужно ответить «да» или «нет». Ему нужно правильно ответить минимум на три вопроса, а он не знает ни одного правильного ответа, но знает следующее:

1) первый и последний вопросы требуют противоположных ответов;

2) не бывает, что на три подряд вопроса ответ один и тот же;

3) не бывает, что утвердительные и отрицательные ответы строго чередуются;

4) последовательность ответов на первые три вопроса не бывает в точности такой же, как последовательность ответов на последние три вопроса.

Помогите Вове сдать тест.

 

5. В телешоу Дом-2013 участвовали 8 юношей и 8 девушек. Каждый юноша поссорился с 14 участниками передачи, а каждая девушка — с 7 участниками. (Ссоры взаимные.) Докажите, что из участников передачи можно сформировать 8 пар, каждая из которых состоит из не поссорившихся между собой девушки и юноши.

 

9 класс

 

1. С натуральным числом разрешается производить следующую операцию: выбрать любую цифру десятичной записи этого числа и прибавить или отнять её (например, из числа 69 можно таким образом получить 63, 75, 60 или 78).

Можно ли за несколько операций из числа 8 получить число 2013? А из числа 2013 получить число 8?

 

2. В квадрате 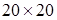  стоят 400 ненулевых чисел. Можно изменить знак у всех чисел, стоящих в одном столбце или в одной строке. Докажите, что за конечное число таких операций можно добиться того, что суммы чисел, стоящих в каждой строке и в каждом столбце, были неотрицательны.

 

3. В каждой вершине куба написано число 1 или -1. На каждой грани записано произведение чисел, стоящих в ее вершинах. Найдем сумму записанных 14 чисел: 8 чисел, стоящих в вершинах и 6 чисел, которые написаны на гранях куба. Может ли эта сумма быть равна нулю?

 

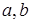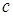4. Докажите, что при любых отличных от нуля числах  и  хотя бы одно из квадратных уравнени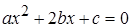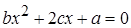й ,   и 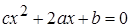 имеет решение.

 

5. Решить в целых числах уравнение .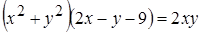

 

10 класс

 

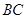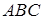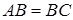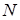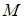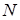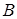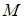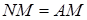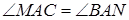1. На стороне  равнобедренного треугольника  () взяли точки  и  ( ближе к , чем ) такие, что  и . Найдите .

 

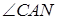2. Катя выписала в строку все двузначные натуральные числа (кроме числа 10) в некотором порядке. Может ли получившееся 178-значное число быть простым?

 

3. Докажите, что нельзя выбрать 100 последовательных чётных чисел и разбить их на пары 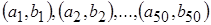 так, чтобы каждый из трёхчленов 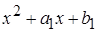, ,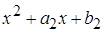…,  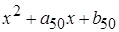имел целые корни. В паре могут быть и не соседние числа.

 

4. На полу лежат 2013 монет. Ровно 19 монет лежат вверх решкой, а остальные — вверх орлом. Требуется с закрытыми глазами разделить все эти монеты на две группы так, чтобы в этих группах находилось одинаковое число монет, повернутых решкой вверх. При этом можно некоторые монеты один раз перевернуть.

 

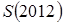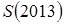5. Сравнить числа  и , где

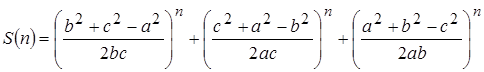, если .

 

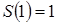11 класс

 

1. Пусть 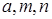 - натуральные числа, причём 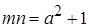. Докажите, что .

 

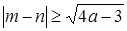2. Супруги Андрей и Оля отправились на вечеринку, на которой присутствовали еще четыре другие супружеские пары. Когда Андрей с женой туда прибыли, они обменялись рукопожатиями с другими людьми. При этом никто не пожал руку самому себе, и ни один муж не пожал руку своей жене. Андрей спросил у каждого, сколько рук он (она) пожал, и получил девять разных ответов. Сколько рук пожала Оля?

 

3. Шесть математиков  обедают. Официант спрашивает: "Все вы хотите кофе?’’

Первый отвечает: "Не знаю’’. Второй отвечает: "Не знаю’’. Третий отвечает: "Не знаю’’. Четвертый отвечает: "Не знаю’’. Пятый отвечает: "Не знаю’’. Шестой отвечает: "Нет’’.

Кому принесут кофе и почему?

 

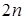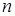4. На плоскости даны  точек. Докажите, что эти точки можно соединить  попарно не пересекающимися отрезками (из каждой точки выходит один отрезок).

 

5. Упростить выражение 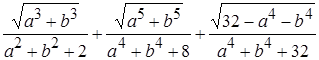, если известно, что .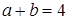